Biểu diễn cấu trúc cây trong cơ sở dữ liệu quan hệ | Phần 1
Thứ sáu, ngày 14 tháng 5 năm 2021Cây là một cấu trúc dữ liệu phổ biến và có ứng dụng rất nhiều để việc giải quyết các vấn đề trong máy tính. Để biểu diễn và cài đặt cây trong bộ nhớ trong khá đơn giản. Vậy việc biểu diễn cây trong cơ sở dữ liệu như thế nào, có khác biệt gì so với khi cài đặt trong bộ nhớ trong, chúng ta cùng tìm hiểu nhé.
Cấu trúc cây
Sau đây là định nghĩa về cây theo Wikipedia
Trong khoa học máy tính, cây là một cấu trúc dữ liệu được sử dụng rộng rãi gồm một tập hợp các nút (tiếng Anh: node) được liên kết với nhau theo quan hệ cha-con.

Ví dụ về một cây nhị phân
Cây có rất nhiều loại, tuỳ thuộc vào đặc điểm cũng như những vấn đề mà nó giải quyết như
- cây nhị phân, cây k phân
- cây nhị phân tìm kiếm - binary search tree
- cây đỏ đen
- cây phân đoạn
- ...
Như hình vẽ, ta có thể dễ dàng mô phỏng một cấu trúc cây như sau
Nút {
khoá
liên kết tới nút cha
dữ liệu
}
hoặc
Nút {
khoá
danh sách các nút con
dữ liệu
}
Chắc hẳn các bạn thường cài đặt theo cách thứ 2 :smile:
Bây giờ, mình cùng nói qua các toán tử chính với cấu trúc cây phổ biến - cây k phân
- thêm một nút vào cây
- xoá một nút khỏi cây
- tìm kiếm một nút trong cây (nâng cao hơn trong thực tế là lấy tất cả cây với nút gốc)
Lưu ý: tất cả đoạn code dưới đây mình sử dụng Python nhé
Biểu diễn cây trong bộ nhớ trong
class Node:
def __init__(self, data: Any, children: List[Node], key: int):
self.data = data
self.children = children
self.key = key
Bây giờ mình sẽ biểu diễn cấu trúc hình bên dưới bằng class Node bên trên nhé
store
├─ book
│ ├─ novel
│ ├─ science
├─ computer/
│ ├─ macbook
│ ├─ dell
store = Node(
data = "store",
key = 1,
children = [
Node(
data = "book",
key = 2,
children = [
Node("novel", None, 3),
Node("science", None, 4),
]
),
Node(
data = "computer",
key = 5,
children = [
Node("macbook", None, 6),
Node("dell", None, 7),
]
)
]
)
Như các bạn thấy, với cấu trúc này khi xoá một nút tương ứng với việc bạn xoá toàn bộ cây với gốc là nút đó, nên ta có thể rút gọn các toán tử tìm một nút từ cây, xoá một nút hay thêm một nút từ cây chỉ là toán tử tìm kiếm một nút.
Với toán tử này, bạn có thể cài đặt một hàm duyệt cây đơn thuần, dfs hoặc bfs để tìm ra nút đó dựa vào key.
Biểu diễn trong cơ sở dữ liệu quan hệ
Lưu ý, phần này là trọng tâm của bài viết :smile:
Như bạn biết rằng, cơ sở dữ liệu quan hệ (SQL) biểu diễn dữ liệu một cách tuyến tính, tức là theo dạng danh sách, để biểu diễn các quan hệ phức tạp, ta cần dùng tới các liên kết được gọi là các quan hệ (khoá ngoại).
Sau đây là ERD cho cấu trúc nút của cây muốn biểu diễn trong SQL
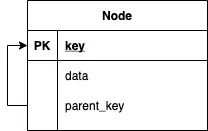
Node trong cơ sở dữ liệu
Do trong một số loại cơ sở dữ liệu quan hệ không có cấu trúc danh sách nên mình không thể biểu diễn danh sách của một nút dưới dạng danh sách con của nó mà mình sẽ làm ngược lại, trỏ nút đó tới cha của nó (cách biểu diễn thứ 1)
Sự khác nhau ở đây là gì? Khi ta có một nút trong tay
- cách 1: ta có thể biết ngay nút cha của nó
- cách 2: ta có thể biết ngay các nút con của nó
OK, đánh giá những khó khăn với các biểu diễn cây trong SQL nhé
- dễ dàng thêm một nút vào cây với độ phức tạp là 0(1) hoặc O(logn) (vì bảng node sẽ được đánh index theo BTree hoặc Hash)
- các toán từ khác sẽ mất thời gian là O(n) hoặc O(nlogn)
Tuy nhiên, có một vài hệ quản trị cơ sở dữ liệu như Postgres hỗ trợ truy vấn đệ quy và bạn có thể truy vấn như sau để có được một subtree của một nút
WITH RECURSIVE nodes_t AS (
SELECT * FROM nodes WHERE key = :key
UNION ALL
SELECT parent_.key, parent.data FROM nodes AS parent
INNER JOIN nodes_t AS child
ON parent.id = child.parent_key
) SELECT key, parent_id, data FROM nodes_t;
còn MySQL thì không có chức năng đó :smile:, ok giờ mình ở đây để giúp các bạn vấn đề này
Vậy làm sao ta có thể tìm tất cả các nút con của một nút cho trước trong 1 truy vấn
Mình có một thủ thuật nhỏ ở đây, ta sẽ thêm một trường hỗ trợ việc này là path
Cấu trúc trường path như sau:
key ông/key cha/key nút hiện tại Lúc truy vấn, ta sẽ truy vấn subtree của một nút có key là store như sau:
SELECT * FROM nodes WHERE path LIKE '%/store/%' OR path LIKE 'store/%';
- điều kiện like thứ nhất sẽ lấy các nút con mà nút
storekhông phải là gốc của toàn bộ cây - điều kiện like thứ hai sẽ lấy nút con mà nút
storelà nút gốc của toàn bộ cây
Yep, chúng ta đã có toàn bộ cây trong subtree, giờ làm sau để đưa nó về dạng 2. Lưu ý, kết quả ta nhận được có cấu trúc như sau
[
{ "key": 2, "data": "book", "path": "store/book", "parent_key": 1 },
{
"key": 4,
"data": "science",
"path": "store/book/science",
"parent_key": 2
},
{ "key": 3, "data": "novel", "path": "store/book/novel", "parent_key": 2 },
{
"key": 6,
"data": "macbook",
"path": "store/computer/macbook",
"parent_key": 5
},
{ "key": 1, "data": "store", "path": "store", "parent_key": null },
{ "key": 5, "data": "computer", "path": "store/computer", "parent_key": 1 },
{ "key": 7, "data": "dell", "path": "store/computer/dell", "parent_key": 5 }
]
OK, giờ các bạn hãy đọc đoạn code sau và suy ngẫm điểm tương đồng nhé
class Node:
def __init__(self, data, children, key, path):
self.data = data
self.children = children
self.key = key
self.path = path
store = Node(
data="store",
key=1,
path="store",
children=[
Node(
data="book",
key=2,
path="store/book",
children=[
Node("novel", None, 3, "store/book/novel"),
Node("science", None, 4, "store/book/novel"),
],
),
Node(
data="computer",
key=5,
path="store/computer",
children=[
Node("macbook", None, 6, "store/computer/macbook"),
Node("dell", None, 7, "store/computer/dell"),
],
),
],
)
def dfs(root):
print(root.path)
if root.children:
for child in root.children:
dfs(child)
print("prefix order")
dfs(store)
print("")
print("sort path by ascend")
paths = [
"store/computer/macbook",
"store/computer",
"store/computer/dell",
"store/book/novel",
"store/book",
"store/book/science",
"store",
]
for path in sorted(paths):
print(path)
Bạn có thể thấy rằng, cách duyệt cây theo thứ tự prefix có kết quả tương tự như cách sắp xếp trường path theo thứ tự tăng dần, và dựa vào đặc điểm này, ta sẽ có hàm xây dựng cấu trúc thứ 2 như sau
Đầu tiên, mình sẽ thêm truy vấn sắp xếp như sau
SELECT * FROM nodes WHERE path LIKE '%/store/%' OR path LIKE 'store/%' ORDER BY path;
Ta sẽ nhận được kết quả
[
{ "key": 1, "data": "store", "path": "store", "parent_key": null },
{ "key": 2, "data": "book", "path": "store/book", "parent_key": 1 },
{ "key": 3, "data": "novel", "path": "store/book/novel", "parent_key": 2 },
{
"key": 4,
"data": "science",
"path": "store/book/science",
"parent_key": 2
},
{ "key": 5, "data": "computer", "path": "store/computer", "parent_key": 1 },
{
"key": 6,
"data": "macbook",
"path": "store/computer/macbook",
"parent_key": 5
},
{ "key": 7, "data": "dell", "path": "store/computer/dell", "parent_key": 5 }
]
def build_tree(flat):
tree = {}
flat.sort(key=lambda x: x["path"])
visited = {}
for item in flat:
key = item["key"]
node = Node(key, item["data"])
visited[key] = node
parent_key = item["parent_key"]
if parent_key not in visited:
tree = node
else:
parent = visited[parent_key]
parent.children.append(node)
return tree
Và đây là kết quả khi cây được build xong
store
book
novel
science
computer
dell
macbook
Bạn có thể tham khảo đoạn code full ở đây
Các bài toán trong thực tế từ vấn đề này như bạn có thể phải trả về cho frontend cấu trúc cây danh mục sản phẩm chẳng hạn, hay một hệ thống quán lí file trên cloud,...
OK, phương pháp này có một hạn chế là phá vỡ lợi ích của SQL đó là chúng ta đã lưu quan hệ của nó vào hai trường (path và parent_key) nên khi chúng ta chuyển nút từ nút cha này sang nút cha khác đòi hỏi chúng ta phải có cơ chế để cập nhật lại trường path. Trong bài viết sai mình sẽ nói về vấn đề này sau.
Mình hi vọng các bạn sẽ thích bài viết này, hẹn gặp lại các bạn trong các bài viết lần sau :smile: